 如何实现减法
如何实现减法
本文内容是《编码:隐匿在计算机软硬件背后的语言》的第13章的内容的总结。主要讲述了计算机系统如何实现减法的这个问题。
加法和减法在某些方面相互补充,但是在机制方面这两个运算则是不同的。加法是始终从两个加数的最右列向最左列进行运算,每一列的进位加到下一列中。在减法中没有进位,而有借位(这是一种与加法存在本质区别的麻烦机制)。
# 十进制减法如何不涉及借位
我们来看一个经典的借位减法:

我们用下面的小技巧让减法不涉及借位。
为了避免借位,首先要从 999 减去减数

由于操作数是三位,所以这里使用 999,如果操作数是 4 位,就用 9999。从一串 9 中减去一个数叫做对9求补数。176 对 9 求补数是 823。反之亦然:823 对 9 的补数是 176。这样做的好处是不需要借位。
计算出减数对 9 对补数后,将补数与原来对被减数相加。
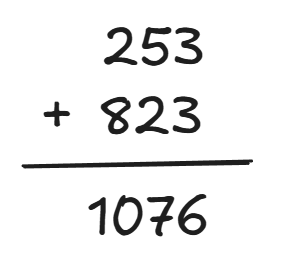
最后再将结果加 1 ,并减去 1000 。
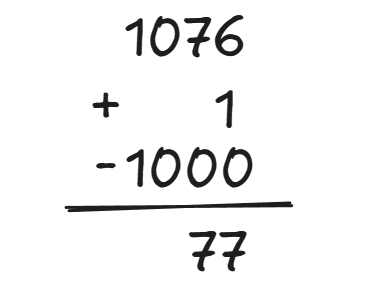
这样就得到最终的结果了,并且过程没有用到借位。
为什么这种方法能行得通?
等价于
组合一下:
这个式子与刚才描述过的计算方式是相同的。我们用两个减法和两个加法来替代一个减法,而在这个过程中避免了烦琐的错位。
# 减数大于被减数
如果减数大于被减数会怎么样呢?
例如下面的这个问题:

你可能会想到,交换两个数,算出结果然后加上负号。其实这样做也会遇到借位问题。
那么如何不使用借位而求解这个问题呢?这就需要采用与之前稍微不同的方法。
使用 999 减去 253,计算出对 9 的补数:

把该数对 9 的补数与被减数相加:

按照前面的例子,下一步应该先加 1,并减去1000得到最终结果。但是这里并不适用。因为会遇到 923 减去 1000 的情况,也会遇到借位。
这里直接减去 999:
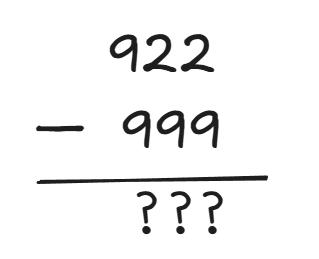
在这里我们再交换减数和被减数,用 999 减去 922,这样就不会使用到借位,其结果也与我们的期望相同:等于 -77
# 二进制减法如何不涉及借位
同样的技巧可以用于二进制数中,而且实际上比十进制数简单。
原题目:

将这些数字转化为二进制数,问题将变为:

用11111111(即255)减去减数:
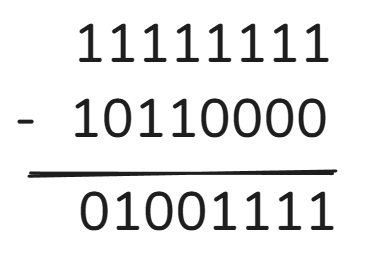
再十进制数减法时,减数是从一串 9 中减去的,结果被称为 9 的补数。在二进制中,减数是从一串 1 中减去的,其结果称为 1 的补数。
但是在求对 1 的补数时其实并没有用到减法:只需要将 1 变为 0, 0 变为 1 即可。因此对 1 求补数有时也会称为相反数或反码。
将减数对 1 的补数与被减数相加:

将上式所得结果加 1:
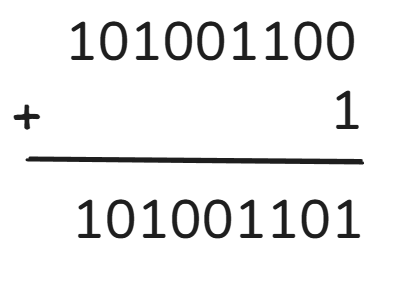
减去 100000000(即256):

其结果就等于十进制的 77。
# 减数大于被减数
我们把这个数颠倒位置再做一遍。在十进制中,减法题目对应于:

而用二进制表示为:

用 11111111 减去减数,得到对 1 的补数:

将减数对 1 的补数与被减数相加:

在被减数大于减数的时候,我们使用先加 1 再减 100000000 来完成计算。
而被减数小于减数的时候。我们先用 11111111 减去上面的结果:

这里我们得到的这个结果是 77,而真正想要的结果应该是 -77。 这是我们一会要解决的问题。
# 改造加法器来实现减法
这里为了不让问题太复杂,这个新的加/减法器只执行在减数小于被减数的减法操作。即结果为正数的情况。
这个加法器的核心是由逻辑门集成的 8 位全加器。
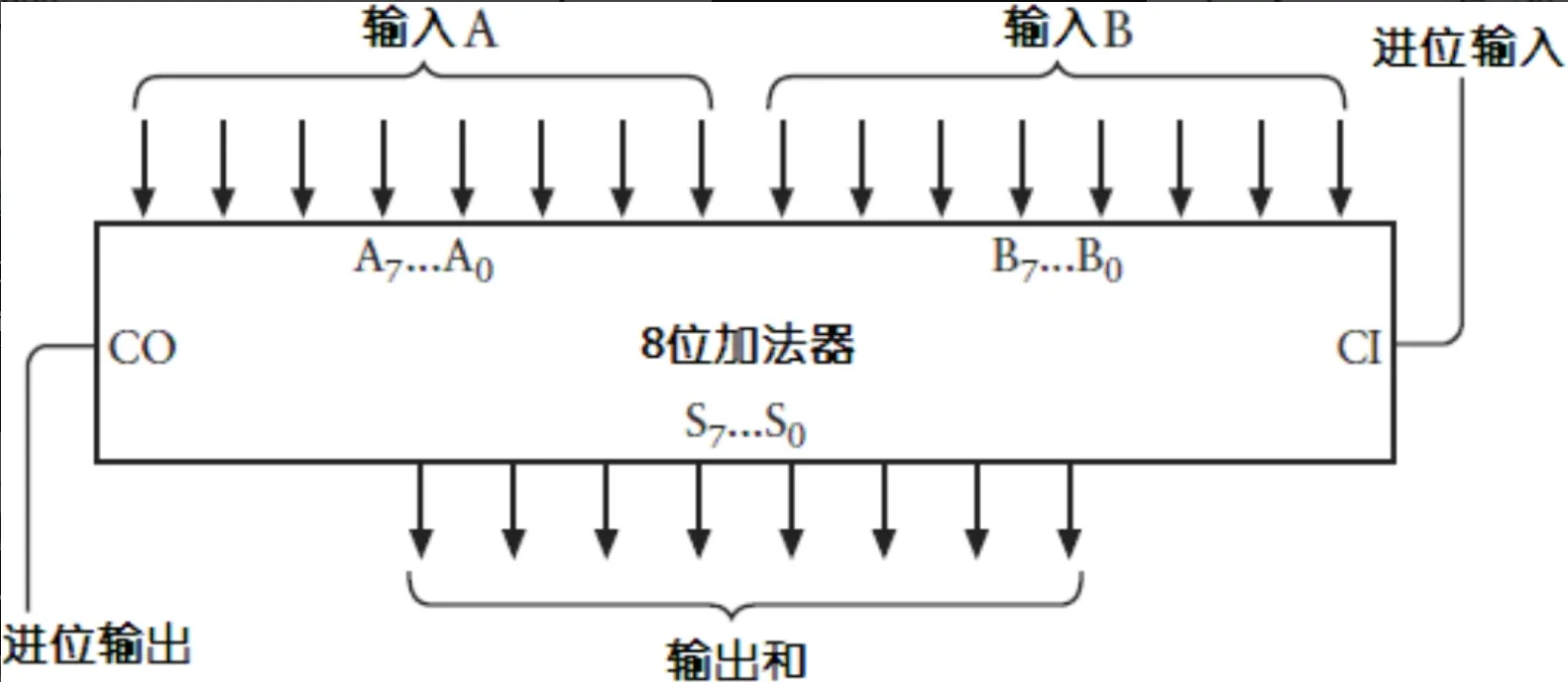
这里输入 A0~A7 和 B0 ~ B7 与两排分别表示两个要相加的 8 位二进制的开关相连。进位输入接地。S0~S7 与表示结果的 8 个灯泡相连。由于这个加法有可能得到 9 位数值,所以进位输入也连接了一个灯泡。
控制面板如图所示:

8 位的加减法器所用的新面板较从前做了些许改动。它增设了一个开关,用于选择做加法还是做减法。

如上图所示,这个开关向下👇表示加法,向上👆表示减法。此外,8 个灯泡表示结果。最左侧的灯泡表示上溢和下溢。上溢(overflow)表示加法中得到了大于 255 。下溢(underflow)表示减法出现了负数。
在加法器上新增的主要部分就是一个用来求 8 位二进制数对 1 补数的电路。之前提到,二进制对 1 求补数相当于对其每位取反,因此我们马上想到计算 8 位二进制数补数的时候可以简单地应用 8 个反向器。
但是如果我们既想做加法又想做减法,就需要当且仅当进行减法运算时才实现反转。电路可以改造为如下图所示:

这里标记为取反的信号将会被输入到每个异或门中。异或门的工作方式如下所示:
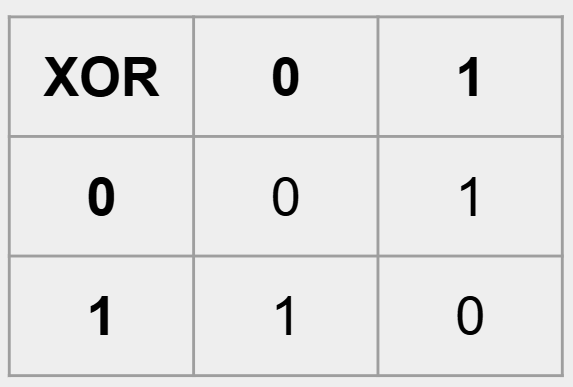
因此,如果 “取反“ 信号为 0,则 8 个异或门的输出与输入相同。如果 “取反” 信号为1,则输出信号将会反置。
将 8 个异或门合并的这个器件,称为求补器,如下图所示:

将一个求补器,一个 8 位二进制加法器和一个异或门做如下连接:

⚠️注意:这里三个信号都标识位 SUB,这就是加/减法转换开关。当该信号为 0 的时候,其进行的是加法运算,反之为 1 的时候,则为减法运算。
在执行减法中,输入B送入加法器之前,需要先通过求补电路进行取反。此外,我们通过设定 CI(进位输入)为 1 来使得结果加 1。而在加法中,求补电路不起作用,且输入 CI 为 0。
加法器的 SUB 信号 和 CO(进位输出)输出作为异或门的输入来控制表示上溢/下溢的灯泡💡。如果 SUB 信号为 0(表示进行加法运算),则当加法器 CO 输出为 1 是灯泡亮,意为加法计算结果大于 255(上溢)。
当进行减法操作的时候,如果减数(输入B)小于被减数(输入A),这时加法器的 CO 端应该输入 1,表示在减法的最后一步中要减去 100000000。而此时SUB也为1,则上溢/下溢灯泡不亮。所以,只有当加法器的 CO 端输出为 0 时,上溢/下溢指示灯才会亮。这表示减数大于被减数,结果为负数。
这样一个加减法器的框架就搭建完成了。
# 二进制如何表示负数
应用二进制的目的在于只希望用 0 和 1 来表示所有的东西,当然也包括负号。
当然,可以简单的用一个二进制位来表示负号,当这一位为 1 时,表示负数,为 0 时表示正数,尽管这样可行,但是还远远不够。比如如何方便负数和正数相加呢?
看下面的数字:

我们可以用如下的表示方法来不用负号表示负数:
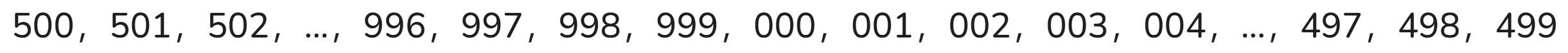
注意,这样就形成了一个循环排序。最小的负数(500)看起来像是最大的正数(499)的延续。而数字 999(实际上是-1)是比 0 小 1 的第一个负数。如果将 999 加 1 ,会得到 1000 。由于我们处理三位数,那个 1 被舍弃,这个结果实际上就是 000 。
这种标记方法称为 10 的补数。为了将三位负数转化为 10 的补数,我们用 999 减去它再加 1 。例如想要得到 -255 对 10 的补数,用 999 减去 255 得到 744,然后再加 1,得到 745。
利用这种补数,我们将不会在用到减法。所有的步骤都用加法来进行。例如 2 - 1,就可用 002 + 999 = 001 就表示 1。
这样的机制在二进制中被称为 2 的补数。以 8 位二进制数为例。范围为 00000000 ~ 11111111,对应这十进制中的 0 ~ 255。但是如果还想表示负数的话,则以 1 开头的每个 8 位数都表示一个负数,如下表所示:

现在所表示的范围是 -128 ~ +127。最左位作为符号位(sign bit)。在符号位中 1 表示负数,0 表示正数。
如何计算 2 的补数:每位取反再加一。例如,十进制的 125 用二进制表示为 01111101,先将 01111101 的每位按位取反,得到 10000010 ,再加 1,得到 10000011 。其实如果在用同样的步骤,每位取反再加 1 ,就可以将数值还原。
这个系统为我们提供了一种不用负号就能表示正负数的方法。同样我们可以自由的将正数和负数用加法法则相加。
⚠️注意的是,这个系统可能涉及了上溢和下溢的情况。即结果大于 127 或者 小于 -128。
笔记
现在,二进制数可以由两种不同的使用方法。可以是有符号的,也可以是无符号的。
