本文内容是《编码：隐匿在计算机软硬件背后的语言》的第11、12章的内容的总结。主要讲述了利用电磁继电器实现逻辑门，以及通过逻辑门实现一个8位加法器。

1. 逻辑门

乔治·布尔（George Boole）是19世纪英国数学家和逻辑学家，他提出了一种新的数学逻辑体系，被称为布尔代数（Boolean Algebra）。布尔代数为计算机科学和数字电路设计奠定了基础，而逻辑门则是基于布尔代数构建的物理实现。

1.1 与门

真值表：

输入都为1，输出才为1。

1.2 或门

真值表：

只要输入有个1，输出就为1。

1.3 非门

真值表：

输入和输出相反。

1.4 或非门

真值表：

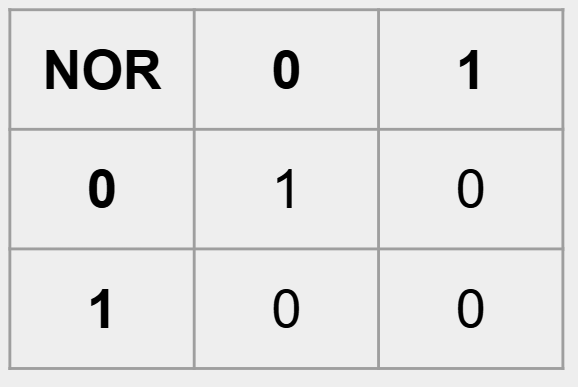
或非门和或门恰好相反。

1.5 与非门

真值表：

与非门和与门恰好相反。

1.6 异或门

真值表：

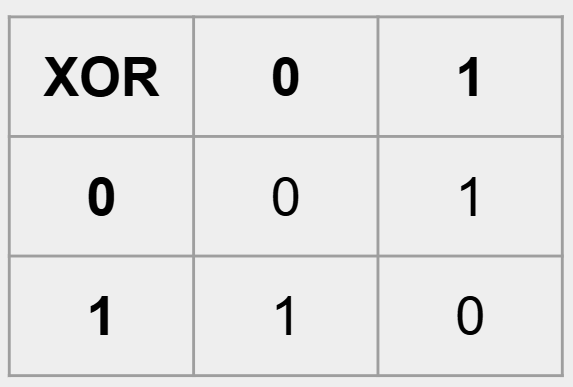
异或门的输入和输出与二进制的加法相似。

1.7 同或门

真值表：

同或门：只有两个输入相同时，输出才为1。正好和异或门相反。

1.8 小总结

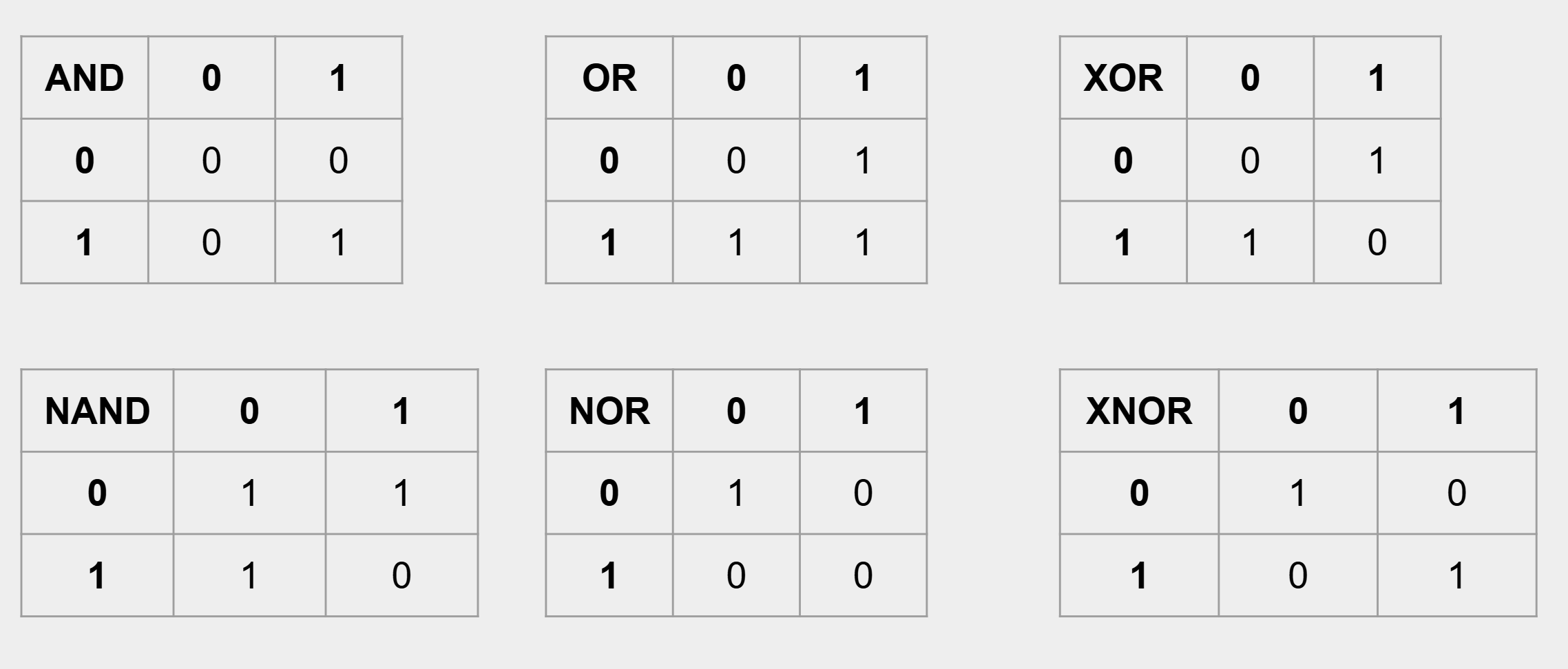
2. 加法器

加法是算术运算中最基本的运算，如果想搭建一台计算机，那么首先就要造出可以计算两个数的和的器件。如果可以制造出加法器，同样我们就可以利用加法来实现减法、乘法和除法...

下面是二进制的加法表：

我们可以将二进制相加拆分为两个数位，一个叫做加法位（sum bit），另一个叫做进位位（carry bit）。

二进制的进位和与门的结果是一致的，可以用与门解决进位问题。

加法位和异或门的结果是一致的，可以用异或门解决加法位的问题。

2.1 半加器

---

为了简化，可以采用如下方式表达：

这个符号被称为半加器。由于半加器没有做到的是将前一次的加法可能产生的进位纳入下一次计算。所以被称为半加器。

例如：假设我们要将如下的两个二进制数相加：

我们只能将半加器用于最右列的一列相加。对于从右面算起的第二列，由于进位位的存在，实际上需要将三个二进制数相加，而随后的每一列的加法都是这样。

2.2 全加器

为了将三个二进制数进行加法运算，我们需要将两个半加器和一个或门做如下连接：

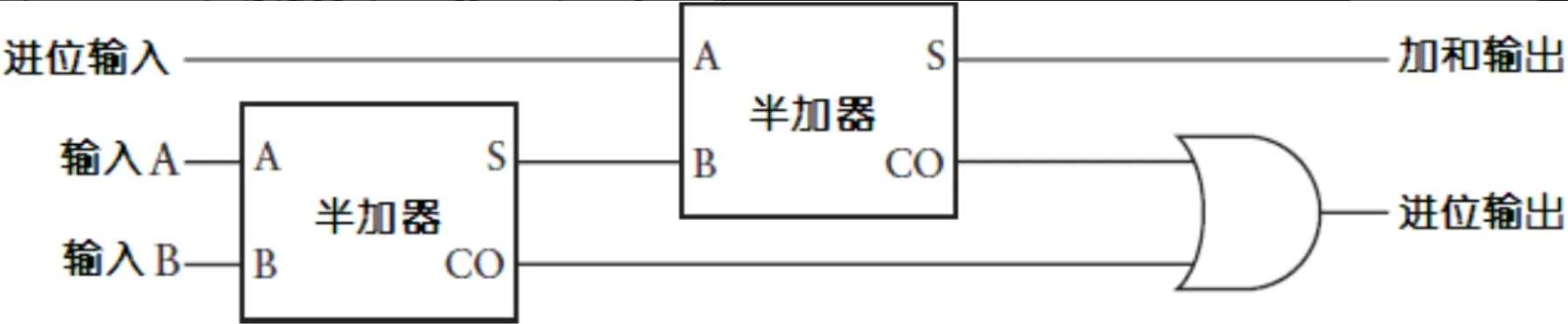
首先从最左边的第一个半加器的输入A和输入B开始，其输出是一个加和及相应的进位。这个和必须与前一列的进位输入相加，然后再把他们输入到第二个半加器中。第二个半加器的输出和是最后的结果。两个半加器的进位又被输入到一个或门中。

👆上面的图可以用下面的符号表示，它被称为全加器（Full Adder）：

以下表格总结了全加法器所有可能的输入组合以及对应的输出结果：

2.3 八位二进制加法器

下面我们设想利用全加器做一个八位二进制加法器。

当把两个二进制数相加时，第一列的处理方式与其他列有所不同。因为后面的几列可能有包括前面加法的进位，而第一列没有。所以全加器的进位输入端时接地的，这表示第一列的进位输入是一个0。第一列二进制数相加后可能会产生一个进位，这个进位输出是下一列加法的输入。

对于接下来全加器和灯泡，可以按照如下方法来连接。

第一个全加器的进位输出就是第二个全加器的进位输入。随后的每列二进制数都是以同样的方式连接。每一列的进位输出都是下一列的进位输入。

最后的第八个灯泡和最后一对开关将以下方式连接到全加器上。

这里的最后一个进位输出被连接到了第9个灯泡上。

用另一种方式来看这8个全加器的连接，每个全加器的进位输出都作为下一个全加器的进位输入。

下面是两种表示这个8位二进制加法器的方式：

---

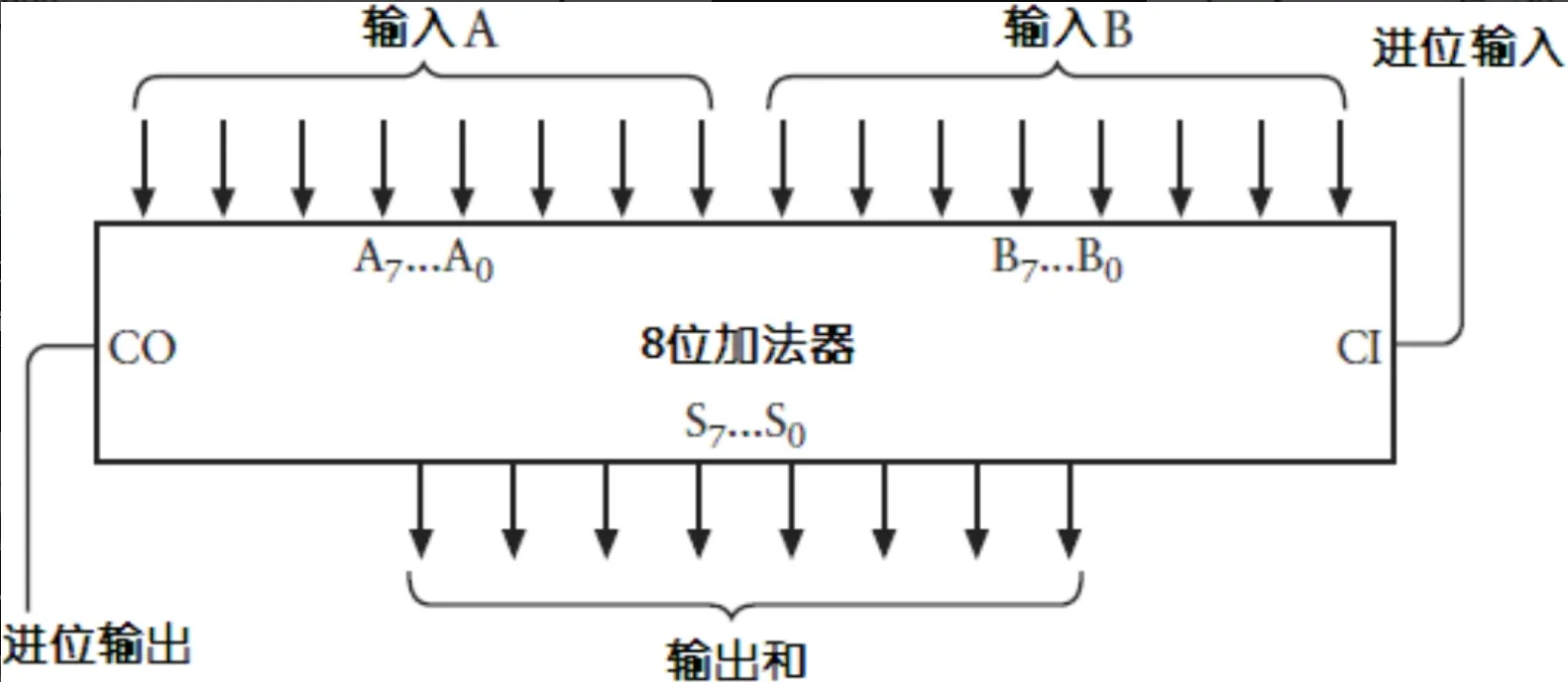
既然已经实现了8位二进制数加法器，不难想到实现一个16位二进制加法器的方法：

笔记

这种加法器的总体速度等于数字的位数乘以全加器器件的速度，这被称为行波进位（ripple carry，或脉冲进位）。更快的加法器运用了一个被称为“前置进位”的电路来提高运算速度。